My Journey into the Fundamentals of Computer Graphics - Part 3

Overview

Hi everyone! This week I continued my journey into the fundamentals of computer graphics by learning about linear & affine transformations. However, before I dive into the things that I learned, I would like to celebrate that today is Programmer's Day 🥳! As part of the celebration, I'm sharing with you this free Fanatical bundle which I just discovered. The bundle includes 4 programming books in pdf & epub format. One of the books included in the bundle is Mathematics for Game Programming and Computer Graphics by Penny de Byl, which is one of the books I've been reading during my journey into the fundamentals of computer graphics. So definitely check out the bundle if you're interested in learning the things that I've learned!

Top 3 things I learned

Watch out for the order of your transformations!

Whenever you're calculating the matrix for a transformation that you want to apply to an object, you need to understand how the library you're using will process the matrix. Otherwise, you'll end up with a different transformation than the one that you expected.

For example, in OpenGL, the transformations are processed in reverse order. This means that if you want to translate, then rotate and then scale an object, in OpenGL you need to first scale, then rotate and finally translate. This is because the multiplication of a matrix with another matrix isn't commutative, which means that the final result will be different.

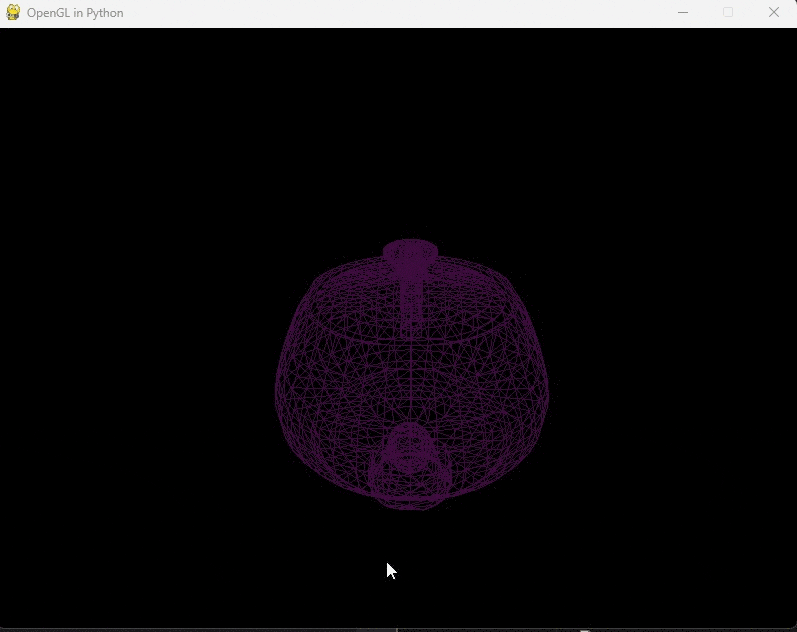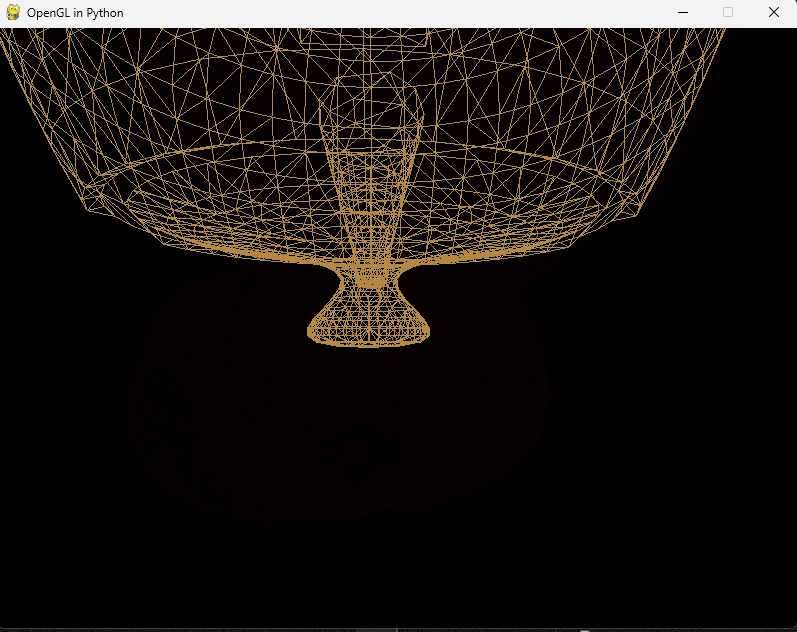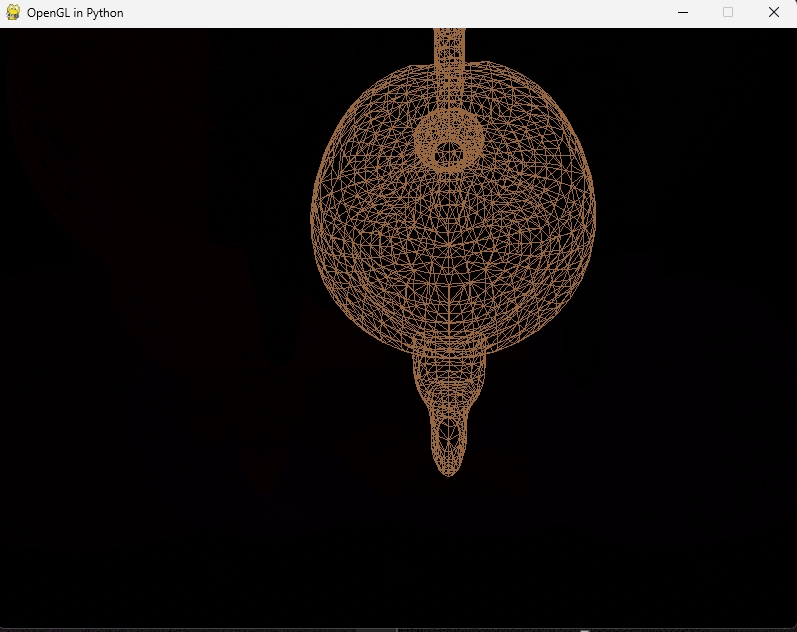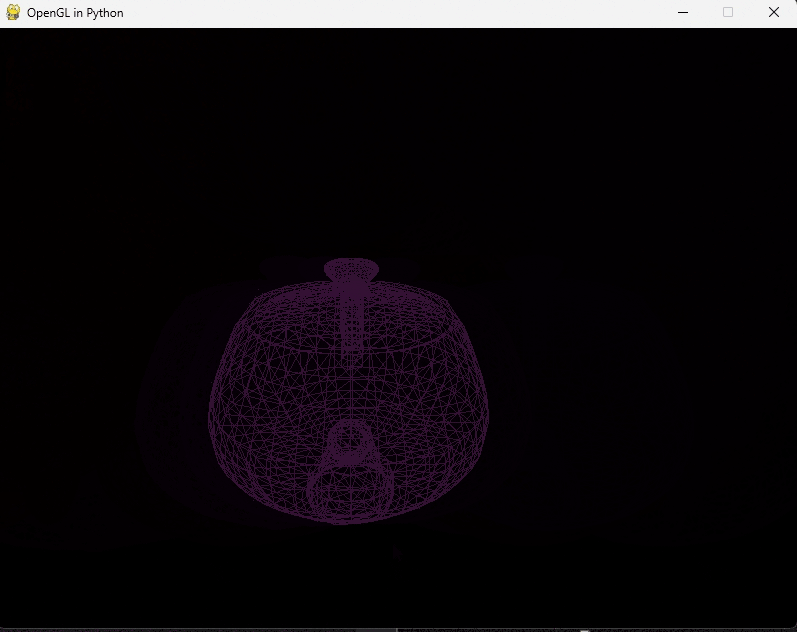
In a very particular example of translating, rotating & scaling an object, if you don't reverse the order of operations in OpenGL, the object won't appear on the screen:

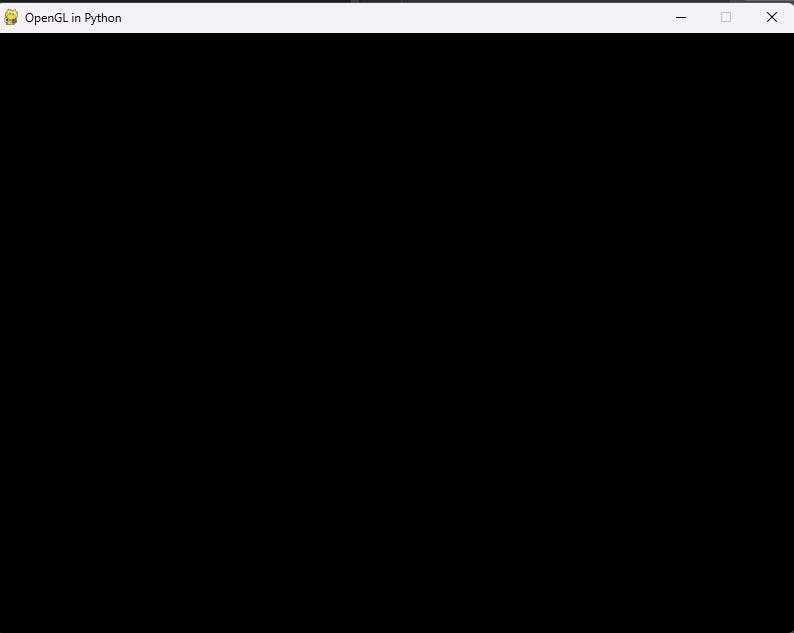
This is the result of the matrix transformation if you don't reverse the order:

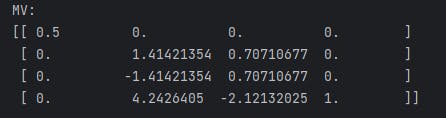
While this is the expected result of the transformation:

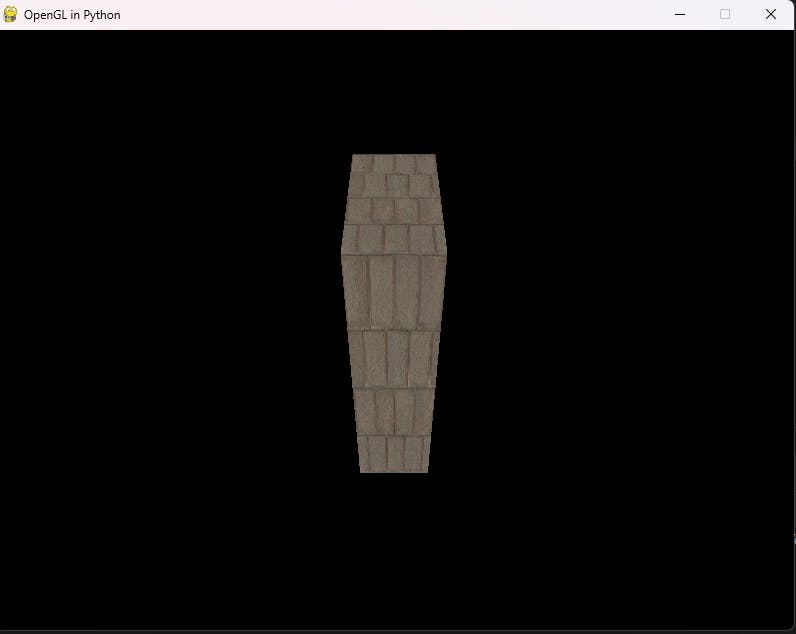
And the expected result on the screen:

Apollo 13, you're heading for gimbal lock...

Out of all the transformations that you can apply to an object, rotation is by far the most complex. This is because a lot of issues arise when you try to do rotations in a 3D space. One of the most common problems is called gimbal lock. This is basically when an entire dimension is lost because you make a 90° rotation in one of the axes and it gets aligned with another axis, which locks them. This was a very big problem during the mission of Apollo 13 to the Moon. Here's a diagram that will hopefully make it more clear:

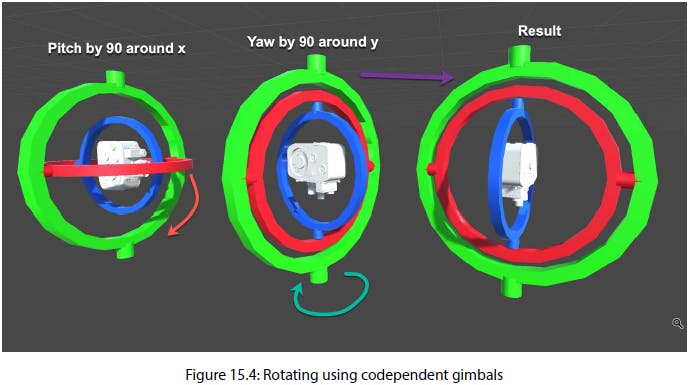
The result of having a gimbal lock in a camera is that it starts to tip roll around the z-axis and it will eventually end upside down.

An approach to first-person cameras

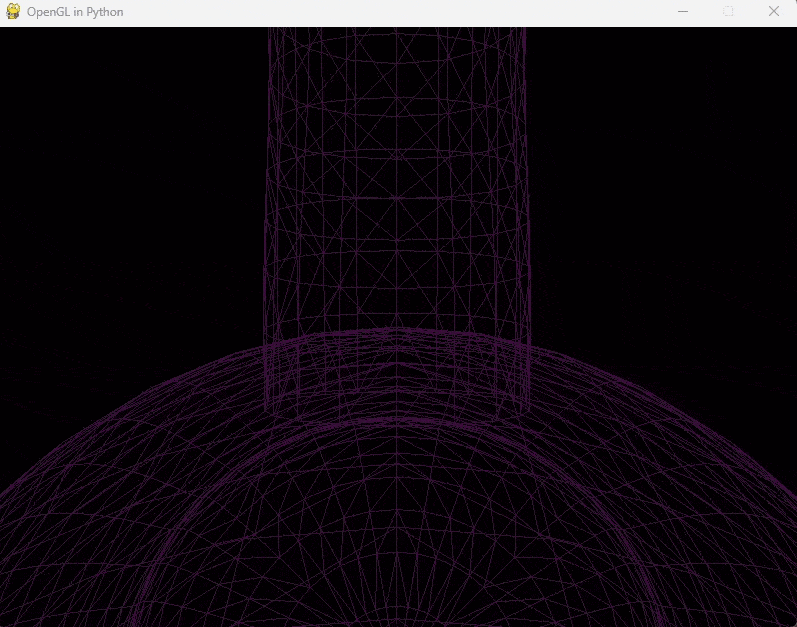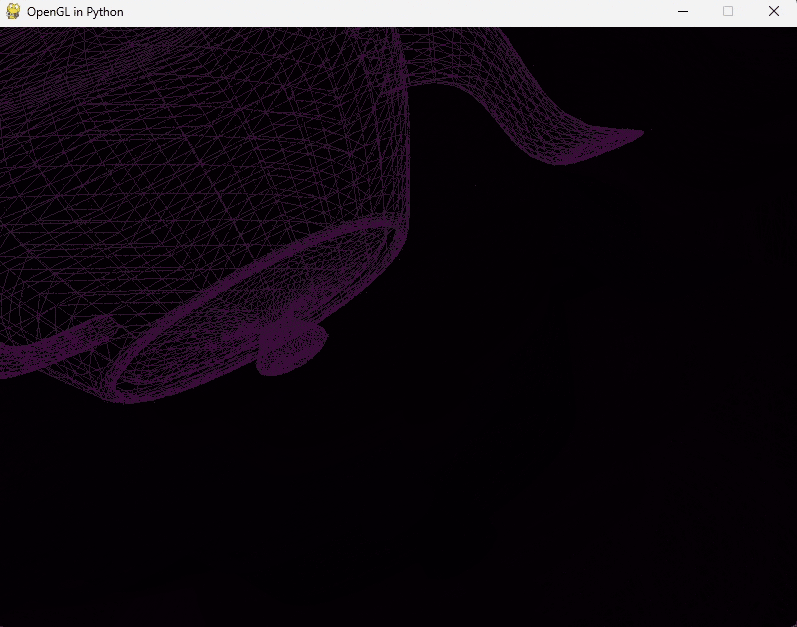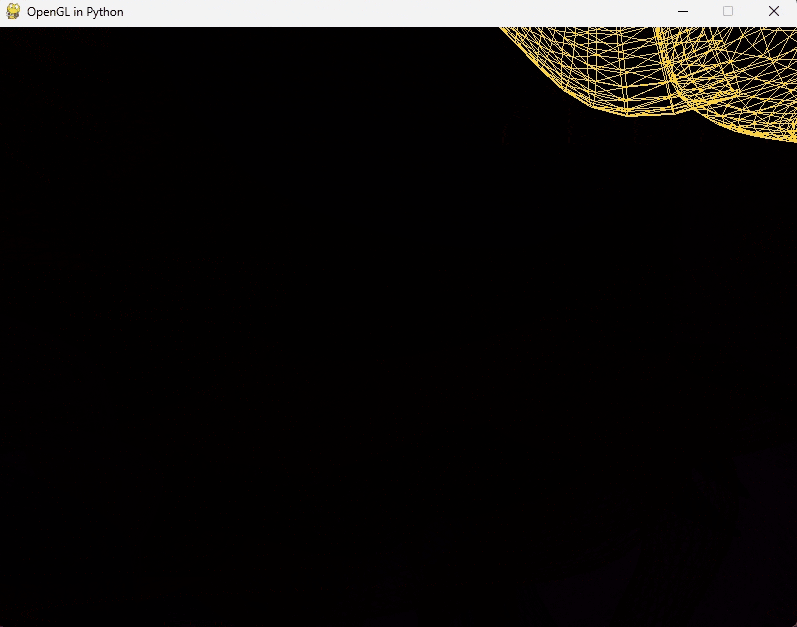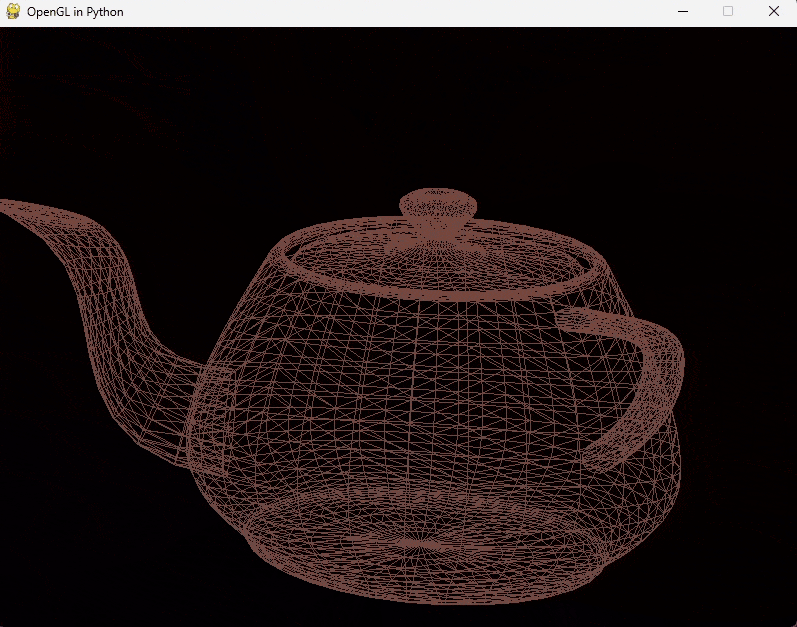
In order to avoid having gimbal locks in first-person cameras, several restrictions are often placed. These restrictions include setting up the controller to rotate around the world's up axis and the camera's forward axis. Which means making switches between local/object & world space. The minimum and maximum angles of rotation for the y and z axes are also restricted to prevent the camera from going upside down. Here's an example of this implementation for a first-person camera:

This week's math concepts

Matrices & Linear Transformations

I learned that the difference between linear transformations and affine transformations is that the former doesn't include translations. This means that affine transformations need to be represented with 4x4 matrices.

I also learned about these 6 linear transformations:

• Translation

• Rotation

• Scaling

• Orthographic Projection

• Reflection

• Shearing

It was also noted that reflection and shearing are usually not used in 3D graphics and they aren't part of a typical graphics API.

More on Matrices

The determinant of a matrix is related to the change in size that results from transforming the matrix. This means that the absolute value is related to the change in area or volume, while the sign indicates if there is a reflection or projection. I learned that the inverse of a matrix allows us to compute the reverse/opposite of a transformation, which can be useful for undoing it. Besides, I also learned about 4x4 homogeneous matrices and how to calculate a perspective projection matrix.

Useful resources

This week, the resources focus mostly on further explanations of matrix concepts and calculators for some of their operations.

• You can learn how to calculate determinants of large matrices in Math Insight.

• You can make quick calculations of determinants with this online calculator.

• You can learn more about matrix math in Math is Fun and Khan Academy.

• You can multiply matrices with this matrix multiplication calculator.

What's next?

You can't possibly expect to solve all the rotational issues that arise in 3D computer graphics by just applying restrictions in the axes. Usually, a better approach for rotations involves the use of quaternions, which is an advanced math concept. This will be my focus for the next week. Meanwhile, I invite you to tell me if you already knew about the gimbal lock and if it has caused you any problems!